After a little more than a semester, I’ve settled on a teaching style that seems to be getting results. In a nutshell, I teach using a combination of very carefully scaffolded worksheets, activities and direct instruction. For Algebra 1, 80% of class time is taken up by worksheets, 10% activities and 10% direct instruction. For Geometry, it’s about 40% worksheets, 40% activities, 20% direct instruction. For Algebra 2, it’s about 40% worksheets, 30% activities and 30% direct instruction. What I’m about to describe definitely won’t work for everyone, but it seems to work for me.
I prefer worksheets over direct instruction because worksheets get my students to do mathematics as opposed to listen to mathematics–there’s nothing like doing mathematics to learn mathematics. Worksheets also allow me to see how every one of my students is performing. There are a number of drawbacks to using worksheets, but I think I have overcome most of them.
The biggest problem is that most worksheets that I’ve seen are horrible. They are usually a bunch of randomly generated problems with no overall structure. Worksheets are often used mainly for students to practice skills rather than to acquire skills. It’s not surprising that worksheets are often seen as busy work and have a bad reputation.
For example, here’s a worksheet from an Algebra 2 textbook on rationalizing radical expressions. I would sequence the problems differently, use different numbers, and probably add some visual aids. I would start with expressions like “6/sqrt(2)” first, rather than “7/(2-sqrt(6))”. Also, I would not choose “2-sqrt(6)” as my first denominator of that type, since (2-sqrt(6))*(2+sqrt(6))=4-6=-2. I would choose a denominator whose product with its conjugate is a positive number. I might even choose something like sqrt(5)-2 since (sqrt(5)-2)(sqrt(5)+2)=1 so that the answer would no longer involve a fraction. I like #21.
I design worksheets to help students practice and acquire skills. Doing this requires precise knowledge of where students are at in their skill development and careful attention to scaffolding, sequencing of problems and design of the worksheet. I’ll describe the general strategy in this post and share specific examples in another post.
Imagine a building with a series of pipes, wood and rope as scaffolding. A less able person trying to reach the top of the building needs more steps and guardrails than a more able person. A less able person guided by an able person needs fewer steps and guardrails than if he were to go alone. Since my goal is to have students acquire skills by completing a worksheet without direct instruction, the scaffolding that is required could be called “microscaffolding”–this is scaffolding with such fine granularity that students almost don’t even notice that they’re moving up from one level to the next.
What does this kind of scaffolding entail? Controlling number of repetitions so that students gain confidence and get enough practice; designing graphical aides, helpful visual elements, mnemonics or other devices to help students learn something, then systematically and slowly taking those elements away until students don’t need them; sequencing problems very carefully so that the level of difficulty or number of steps or number of skills involved slowly increases.
Also, it’s important to choose good numbers problems and examples. Such things have a huge effect and it surprises me that I don’t hear more teachers talking about it. For example, you wouldn’t want to have students see (x+2)^2 as the first example of expanding the square of a binomial because the answer, x^2+4x+4, has two fours, one being the result of 2+2 and the other being 2*2. (Homework for readers: What is first line that you would have students graph and why?) After teaching high school for a short while, I have definitely gained appreciation for the difference between mathematical content knowledge and mathematical content knowledge for teaching.
Another thing that I like to do is to hide patterns in the answers or problems on the worksheets. I usually walk around the room while students are working and ask them about the patterns they’re observing. Here’s an example.
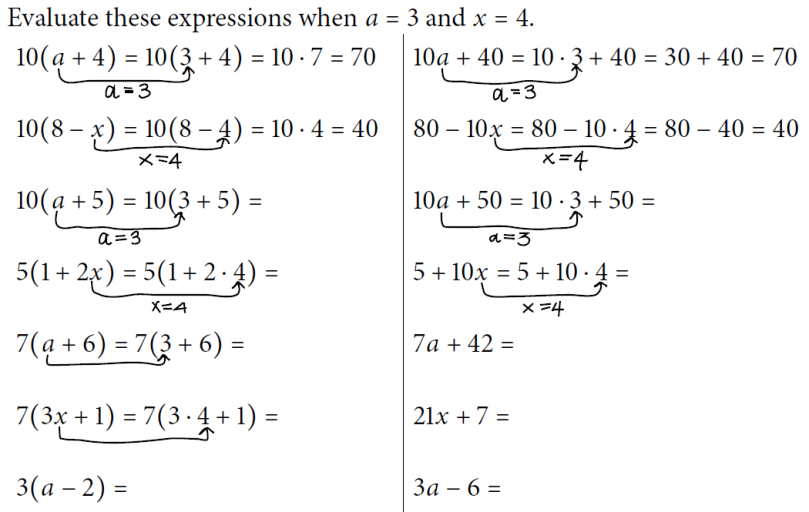
This worksheet for Algebra 1 involves substituting numbers into expressions and order of operations. The answers on the left come out to be the same as the answers on the right because the answers on the right are expanded versions of the expressions on the left. However, students had not yet learned about the distributive property at this point in class. A few students were able to figure out why the answers matched.
I don’t usually have a problem with getting students motivated to work on this kind of worksheets. Students can tell that this isn’t just busy work. They feel successful when they work on them and thereby build intrinsic motivation to work on mathematics. And, I believe that most students have untapped curiosity that drives them to like to figure out patterns. So, I don’t have to struggle with finding context for the problems that I give–I give lots of “naked” math problems and students don’t seem to mind that.
Using so many worksheets means that I go through a lot of paper. Huge amounts of paper–several pieces of paper per student per class. Putting aside the problem of acquiring or buying paper and having to make so many copies, there’s the problem of having collect and grade so much paper. Fortunately, I tend to grade work very quickly and so I am able to provide feedback to students in a timely manner. The management of paper can also be troublesome, but I’ve come up with a filing system that works for me.
One other issue is that this kind of work is very time consuming. Creating these worksheets takes time and because I’m so particular about the visual layout of words, symbols and diagrams on worksheets, it takes even more time. I design most worksheets and activities from scratch using LaTeX and Adobe Illustrator. I use these programs so that I can have complete control over layout of the worksheet. I am very picky about white space on worksheets and font size–students don’t feel as intimidated when the font is large and there are fewer problems per page. After they become a bit more comfortable with the math, they can handle smaller fonts and more problems per page. If you give a student a worksheet with 50 problems on a page and another student a set of 5 worksheets with 10 problems per page, I would bet that the latter would finish faster and more successfully.
Finally, I should mention that this idea of “microscaffolding” is not new and not my own creation. I first got introduced to this idea through Kumon, a math and reading enrichment program with franchises around the world. The secret of Kumon is its worksheets, which are so exquisitely designed that students learn mathematics essentially by themselves. I worked a number of Kumon centers during my middle and high school years.

Fascinating read, profteacher! I went through (and loathed, unfortunately) a few years at Kumon, and I can attest to the program’s efficacy.
I’ve started making worksheets for my linear and discrete math recitation sections (kinda like 55, but with some basic linear programming and algorithms stuff thrown in). They are not as carefully designed as yours are (I don’t think I know enough teaching theory to make them as carefully designed as yours are – even if I had time), but they seem to be helping the students to be more engaged anyway :-). I should learn more about this microscaffolding thing…
Is this an opportunity for the computer to play a role here? If the students are doing the worksheets to learn, they can get immediate feedback on their grasp of each micro concept as they enter their answers into a computer-based worksheet as to whether they are right or not. This also may solve the problems of too much paper use and also grading load. However, not being in education myself, I am just in the peanut gallery. You probably don’t have computers in the classroom for each student but maybe you can argue a case for it.
There are software companies that are trying to do exactly that right now. Let’s hope they are effective!
This is the sort of work you shouldn’t have to do — a well-written curriculum should do this for you! Your ideas around “good” rat the den problems are right on target of course. I also like to give ones with common factors, like (10 + 5 sqrt 2) / (2 + sqrt 2).
There’s a big benefit to writing problems this way, which is that kids start to look for connections between problems, and common themes running throughout. This goes well with the core math idea that ideas and skills build over time and connect, which is somehow missed by a ton of kids.
Hopefully over time you won’t need to microscaffold as much as you do, and kids may be able to come up with some of the scaffolding for themselves. That is definitely a long term goal though, and my preference is to scaffold too much instead of too little.
For factoring I’ve had good luck with x^2 + 7x + 10 and x^2 + 10x + 21 as starters; however my actual starter tends to be the more direct “Find me two numbers whose sum is 10 and whose product is 21”, then later build the connection to the expanded form. For lines, the first line in our Algebra 1 textbook is x = 2, the second is y = 5, and the third is 2x + 3y = 12. What did you have in mind? (Note none of these are in the dreaded y = mx + b form, and are all introduced before the chapter called “Lines”.)
Try not to worry so much about layout – there just isn’t time. I say this as a picky layout guy, though. Ideally you want the worksheets you build to be usable and editable by other teachers, electronically or not. For that reason I wouldn’t use TeX, but if it’s what you are comfortable with, no biggie.
Keep it going, dude! See you this summer for 3 weeks of scaffolding.
– Bowen
[…] Comments (RSS) « Microscaffolding […]